偏差値って何?
学生時代によく聞いた「偏差値」という言葉。
私の場合大抵は「偏差値」という言葉が出るときは楽しくない場面が多かったです。
自分の得点が平均値と同じなら偏差値は50ということですから、偏差値40台なら「もうちょっと頑張らないと」とか、偏差値50を超えると「ひとまず安心かな」といった感覚がありました。
でも心の何処かに「どうしてテストの点数ではなくて偏差値にばかり注目するのだろう」という引っ掛かりがいつもありました。
今回学び直して、「偏差値」がどういうものかがわかりましたので、このノートに記しておきます。
計算方法は後回しにして結論からいうと、「偏差値」とは平均値からの離れ具合をみんなと比べた、ということでしょうか。
「みんなと比べてどのくらいヤバい(またはスゴい)の?」を測る指標だということですね。
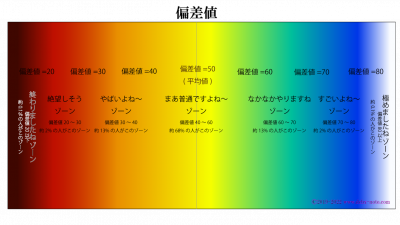
全員の中での位置関係
平均値からの「離れ具合」ということであれば、たとえば平均値が54点、自分の得点が40点だとすると、「平均から14点離れている(下回っている)」ということですが、これですと平均点と自分の得点を比べているだけのことになります。
偏差値というのは、
”自分の得点の平均値からの離れ具合が他の人たちの得点の平均値からの離れ具合と比べてどうなの?”
といういうことを知るためにあるのです。
まだピンと来ませんよね。
実際のデータで見てみましょう。
シナリオで見る偏差値
100人のクラス
実際の学校で100人のクラスは見かけませんが、なんとなく切りが良いので100人のクラスでテストをしたと仮定します。
テストの結果、私の得点は40点でした。
恥ずかしいと思いたいところですが、点数だけではレベルがわからないので、偏差値を見てみましょう。
シナリオ1:平均点は50点(その1)
平均点を聞くと50点とのことでした。
偏差値は44.6でした。
「平均よりちょっと少なかったな。次はちょっと頑張らないとね」
シナリオ2:平均点は50点(その2)
こちらも平均点は50点。
ところが偏差値はなんと30.5だったんです。
「かなりまずい状況だよね。死にものぐるいで頑張らないと!」
シナリオ3:平均点は30点(その1)
平均点は30点でした。
得点が40点でしたのでがっかりしかけましたが、平均よりは多かったです。
偏差値は56.5でした。
シナリオ4:平均点は30点(その2)
さきほど同様平均点は30点でした。
ところが偏差値は69.1なんです。
「点数は低いかと思ったけど、努力の甲斐があったよ」
どのシナリオも得点は40点なのに偏差値には大きな違いがありました。
| 平均点 | 偏差値 | |
|---|---|---|
| シナリオ1 | 50点 | 44.6 |
| シナリオ2 | 50点 | 30.5 |
| シナリオ3 | 30点 | 56.5 |
| シナリオ4 | 30点 | 69.1 |
偏差値って一体・・・
各シナリオの得点分布
それぞれのシナリオについて、クラスの得点分布を見てみましょう。
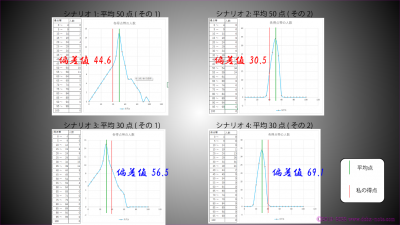
得点の分布(低い得点と高い得点の範囲)が広い場合、私の得点と平均点の離れ具合(つまり偏差)は大きくありませんが、得点の分布が狭い場合、私は他の人に比べて平均点からの離れ具合が大きいということです。
偏差値と標準偏差
ここまでは偏差値について難しい単語や計算式に触れずに書いてきました。
同じ40点でもクラスのみんながどんな点数を取るかで偏差値が変わってくるということのイメージをつかんで頂きたかったのです。
ここからは偏差値の算出方法に迫って行きたいと思います。
まず偏差値を算出するために絶対に必要になるのが標準偏差なのです。
標準偏差? 偏差値と同じように「偏差」という言葉が入っているので混乱しそうですね。
記事の冒頭で、偏差値とは
”自分の得点の平均値からの離れ具合が他の人たちの得点の平均値からの離れ具合と比べてどうなの?”
と書きました。
この文章を2つに分けますね。
前半の「自分の得点の平均値からの離れ具合」というのが偏差値、
後半の「他の人達の得点の平均値からの離れ具合」が標準偏差なのです。
つまり偏差値というのはクラスの人たちそれぞれが持っている値ですので、100人クラスでは100個の偏差値があるわけです。
それに対し、標準偏差はクラス全員の離れ具合の標準的な基準として算出した値ですので、クラスに1つの値しかありません。
この記事では標準偏差よりも偏差値という単語の方が先に登場してしまいましたが、そもそも各生徒の偏差値はクラスの標準偏差から算出するものなのです。
標準偏差
繰り返しになりますが、標準偏差とはクラス全体の平均値の離れ具合を標準的な値として算出したものです。
平均点との差は生徒によってまちまちですよね。
平均点近くの人、平均点を大きく下回っている人、平均点を大きく上回っている人・・・
自分の得点が他の生徒と比べてどうなのかを知るためにクラスメート一人一人に「君何点だった?」って聞いて回るのは大変です。
そこで標準的な「離れ具合」の値と自分の離れ具合を比較すれば自分のテストの出来栄えを把握しやすくなります。
ちょっと難しくなりますが、標準偏差の計算に入っていきましょう。
標準偏差の計算方法
100人のクラスでは計算が大変ですので、10人のクラスを作ってみました。
各生徒の得点は次のとおりです。
| 生徒番号 | 得点 |
|---|---|
| 1 | 40 |
| 2 | 53 |
| 3 | 57 |
| 4 | 42 |
| 5 | 44 |
| 6 | 43 |
| 7 | 48 |
| 8 | 45 |
| 9 | 39 |
| 10 | 31 |
①平均
まず平均点を算出します。
これは簡単ですよね。
(40+53+57+42+44+43+48+45+39+31)÷10 = 44.2
②平均値との差
次に各生徒の平均値との差を出します。
| 生徒番号 | 得点 | 平均点との差 |
|---|---|---|
| 1 | 40 | -4.2 |
| 2 | 53 | 8.8 |
| 3 | 57 | 12.8 |
| 4 | 42 | -2.2 |
| 5 | 44 | -0.2 |
| 6 | 43 | -1.2 |
| 7 | 48 | 3.8 |
| 8 | 45 | 0.8 |
| 9 | 39 | -5.2 |
| 10 | 31 | -13.2 |
③平均値との差の2乗
各生徒の平均値との差を2乗します。
なぜ2乗するのかはここでは説明を割愛します。
| 生徒番号 | 得点 | 平均点との差 | 平均との差の2乗 |
|---|---|---|---|
| 1 | 40 | -4.2 | 17.64 |
| 2 | 53 | 8.8 | 77.44 |
| 3 | 57 | 12.8 | 163.84 |
| 4 | 42 | -2.2 | 4.84 |
| 5 | 44 | -0.2 | 0.04 |
| 6 | 43 | -1.2 | 1.44 |
| 7 | 48 | 3.8 | 14.44 |
| 8 | 45 | 0.8 | 0.64 |
| 9 | 39 | -5.2 | 27.04 |
| 10 | 31 | -13.2 | 174.24 |
④分散
各生徒の③の値を平均します。
これを分散と呼んでいます。
(17.64+77.44+163.84+4.84+0.04+1.44+14.44+0.64+27.04+174.24)÷10 = 48.16
⑤標準偏差の算出
分散の平方根(√)が標準偏差です。
√48.16 = 6.94
偏差値
標準偏差が6.94とわかったところで各生徒の偏差値を出すことができます。
この6.94が標準偏差の1単位だと思ってください。
1単位が偏差値10に相当します。
自分の得点が、
- 平均点と得点が同じなら偏差値50
- 平均点より1単位だけ低ければ偏差値40
- 平均点より2単位低ければ偏差値30
- 平均点より1単位高ければ偏差値60
- 平均点より2単位高ければ偏差値70
ということです。
計算式で表すと次のようになります。
(得点 – 平均点) ÷ 標準偏差 × 10 + 50
言葉で表すと、自分の得点と平均点との差が標準偏差の何倍あるのかというのが偏差値の考え方ですね。
各生徒の偏差値を見てみましょう。
| 生徒番号 | 得点 | 偏差値 |
|---|---|---|
| 1 | 40 | 43.9 |
| 2 | 53 | 62.7 |
| 3 | 57 | 68.4 |
| 4 | 42 | 46.8 |
| 5 | 44 | 49.7 |
| 6 | 43 | 48.3 |
| 7 | 48 | 55.5 |
| 8 | 45 | 51.2 |
| 9 | 39 | 42.5 |
| 10 | 31 | 31.0 |
おまけ
先に示した各シナリオの絵に標準偏差の線を加えてみました。
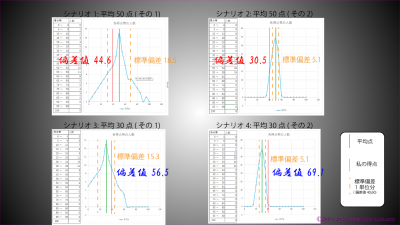
まとめ
いかがでしたか?
偏差値というもののイメージをつかんで頂けましたか?
インターネットで偏差値を検索すると、大抵は算出のための公式から入っていたり言葉が難しかったり。
今回この記事ではできるだけ難しい表現を使わないようにしてみました。
記事内で使った100人クラスのシナリオに使ったデータをExcelファイルで添付しておきますので、興味のある方はいろいろ触って偏差値の理解を深めてください。
偏差値算出のためのシナリオExcel(hensachi.xlsx)
あとがき
そもそも私がなぜ今偏差値を学習しようとしたかと言いますと、最近株やFXの研究を始めたからです。
株やFXに関する書籍やインターネットの情報には必ず「ボリンジャー線」という表現が出てきます。
ボリンジャー線は今後の値動きを予想する際に参考とする曲線なんですが、私はその曲線の意味するところや算出方法を知らなかったのです。
ボリンジャー線というのは実は標準偏差(をもとにした曲線)なんだということがわかり、そう言えば偏差値という言葉があったけど標準偏差とは別物?という疑問が湧いてきました。
私はそもそも頭が良くない(偏差値が低い)ので、自分なりにノートに書きながらやっと理解できました。
せっかく理解できたのだから忘れないうちに記事にしておくことにしました。
長い文章になりましたが、最後まで読んでいただきありがとうございます。



コメント